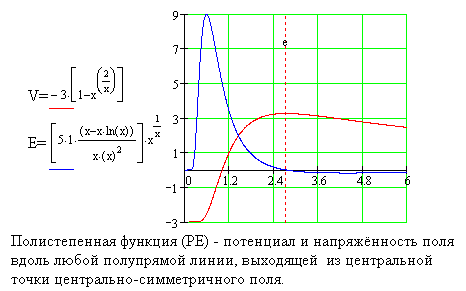
Законы динамики Ньютона.
Смотря с некоторой точки зрения, можно увидеть, что три закона динамики это в сущности есть один закон, который был расписан на "три точки". С этой точки зрения второй закон динамики - который гласит, что сила есть пропорциональна ускорению, которого она является причиной - есть только определением силы. Попросту, это определение представляет собой предложение "научного договора" - оно предлагает, чтобы при помощи слова "сила" называть некоторое произведение, а именно, сила F=m*a.

С которой точки зрения это видно? Это видать, если за основу для размышлений принять гравитационный закон Галилея, который гласит, что в гравитационном поле все тела падают с одиноковыми ускорениями. Это означает, что ускорение падения тел с разными массами не зависит от масс этих тел, а зависит от поля и массы тела, которое является причиной ускорения для падающих тел. Поэтому при выборе подходящей функции для описания центрально-симметричного (ц.с.) поля достаточно, чтобы ускорение было пропорционально величине массы ускоряющего тела, а тогда остальная часть функции может иметь любой вид.*)

Пусть ускорение описывается при помощи формулы E=M*Ej - это одновременно есть формула, описывающая напряжённость поля, которое является причиной ускорения. Это есть формула, описывающая ускорение и напряженность поля вдоль любой полупрямой, которая "выходит" из центральной точки поля. В этой формуле М есть массой тела (поля), которое есть - гипотетической, а не действительной(!) - причиной ускорения, а Ej это ускорение (других тел), происходящее от тела с единичной массой, т.е. когда в формуле E=M*Ej подставить М=1, получается Ej=1*Ej.

Следовательно, ускорение тела в поле с массой М1 равняется E1=M1*Ej, а ускорение тела в поле с массой М2 равняется E2=M2*Ej. Пусть два тела с массой М1 и М2 находятся на некотором расстоянии друг от друга и придают друг другу ускорения. Тогда тело с массой М1 будет иметь ускорение E2=M2*Ej, а тело с массой М2 будет иметь ускорение E1=M1*Ej. А какое в таких случаях будет произведение массы ускоряемого тела и его ускорения?

Для тела с массой М1 произведение массы и ускорения равняется M1*E2=M1*M2*Ej (ибо причиной ускорения является тело с массой М2), а для тела с массой М2 произведение массы и ускорения будет равно M2*E1=M2*M1*Ej (ибо причиной ускорения является тело с массой М1). Здесь можно заметить, что эти произведения равны друг другу.

Если здесь применить определение - т.е. содержание второго закона Ньютона - которое говорит, что F1=M1*a1 и F2=M2*a2 (при том a1=E2 и a2=E1), тогда можно записать, что F1=M1*M2*Ej и F2=M2*M1*Ej. Обычно в математическом описании учитываются противоположные направления ускорений тел с массой М1 и М2, следовательно, в описании это равенство представляется в виде F1=-F2. Это равенство называется третьим законом динамики - его можно пересказать словами: взаимодействия двух тел друг на друга равны и направлены в противоположные стороны.

Новые законы динамики.
Здесь надо на момент вернуться на место в тексте, которое обозначено как *). Там говорится о том, что остальная часть функции ускорения ц.с. поля E=M*Ej, то есть, часть записана как Ej, может иметь любую структуру. Но надо здесь обратить внимание на то, что в логичном выводе (и определении) формул, которые находятся в законах динамики Ньютона, используется только одна такая часть, а не разновидные. То есть, везде используется та самая часть Ej, а не части Ej1, Ej2, Ej3... Говоря по-другому, та часть функции может обладать разновидной структурой, но для логичного вывода законов Ньютона принимается часть c одной структурой, которая в выводе не изменяется.

В таком случае можно сказать, что для вывода зависимостей, которые известны как законы динамики Ньютона, по умолчанию принимается постулат, который говорит, что все ц.с. поля изменяются по одной и той же математической формуле. Самым важным следствием этого постулата является то, что законы динамики Ньютона есть аккурат такие, какие есть. То есть, в процессах, которые протекают с соблюдением законов динамики Ньютона, общий центр тяжести объектов остаётся неподвижен и не меняется количество энергии системы.

Но можно ожидать, и многие факты указывают на то, что природа обладает и "другой стороной медали", которая описывается законами, опирающимися на другом постулате. В этом другом постулате часть функции ускорения, обозначаемая как Ej, для разных ц.с. полей имеет разновидную математическую структуру, то есть, для разных ц.с. полей она должна записываться как Ej1, Ej2, Ej3... В таком случае, в процессе с такими объектами, как бы по поводу природы ц.с. полей (объектов), общий центр тяжести движется самодейственно и, разумеется, самодейственно меняется количество энергии системы.
 

Общий корень всех законов динамики.
Компьютерная исполнительная программа  Gravo2S.exe  предназначена для графично-динамического иллюстрирования как законов динамики Ньютона, так и законов динамики СДВ (самодейственного движения вещества). И одни, и другие законы в этой программе представляются одинаковым образом. А именно, тела (частицы, центрально-симметричные поля) ускоряют взаимно друг друга на одном и том же принципе - можно также сказать, что в их поведении проявляет себя Фундаментальный принцип вещества.

В программе Gravo2S - на его экране - можно наблюдать поведение двух частиц на фоне графика потенциала своего соседа. На основе наблюдений можно сформировать заключения. График потенциала, а также сам потенциал, это лишь некоторого вида понятийно-математический приём. Потенциал и его график полезны здесь в той степени, на сколько возможно их использовать как отображение некого физического объекта. А сам этот физический объект можно потрактовать как оправдание и причину, если надо будет объяснять (если кто-нибудь бы спросил), откуда происходит движение частиц. Тогда явление можно объяснять таким образом, что ускорение происходит вследствие воздействия потенциального поля соседней частицы. При том, центрально-симметричное поле и частица это одна и та же вещь, только она определяется другими словами.

Потенциал поля и само центрально-симметричное поле это вторичные понятия и вторичные физические объекты, которые надо понимать как дедуцированы на основе какого-то первобытного понятия и физического объекта. Этим первобытным понятием и объектои(!) является движение и ускорение, которое можно представить при помощи математической функции. В действительности, не известно, что такое там движется. Но движется... Ибо эта вещь - сама двигаясь, при влиянии каких-то в начале не известных для нас причин - движет нашими чувствами. На этой основе мы научились распознавать разные вещи и их называть. Идентичным образом определяется движение и само существование объектов в виде центрально-симметричных полей... либо частиц, либо тел.

Математическая функция ускорения частицы называется также функцией напряжённости поля, которое то поле, в формальном отношении, является причиной ускорения частицы. Но следует здесь отличать друг от друга эти две вещи. Потому что функция ускорения есть связана с движущейся частицей и её касается, зато функция напряжённости поля касается частицы, которая есть причиной ускорения этой движущейся частицы.

Математическая функция ускорения, или иначе, функция напряжённости поля (ибо в отношении математической структуры это есть та же сама функция), в математическом и формальном отношениях есть связана с функцией потенциала поля, то есть, с распределением этого поля в пространстве. Потенциальная функция поля возникает как результат интегрирования функции напряжённости поля; или можно сказать по-другому, что функция напряжённости поля является производной от функции понтенциала поля.

Именно по поводу этих математических зависимостей, во время наблюдения поведения частиц на экране программы Gravo2S, так красиво синхронизированы их движения на фоне графиков потенциального поля своих соседок.

В программе Gravo2S можно наблюдать частицы, движущиеся в соответствии с функцией ускорения. Эта функция выступает в нескольких видах. Она может иметь вид полистепенной функции или полистепенной суммированой функции. Полистепенные функции (PE) и полистепенные суммированые функции (PES) отличаются тем, что при их помощи можно создавать модели стабильных структурных систем - наиболее простая система состоит из двух частиц.

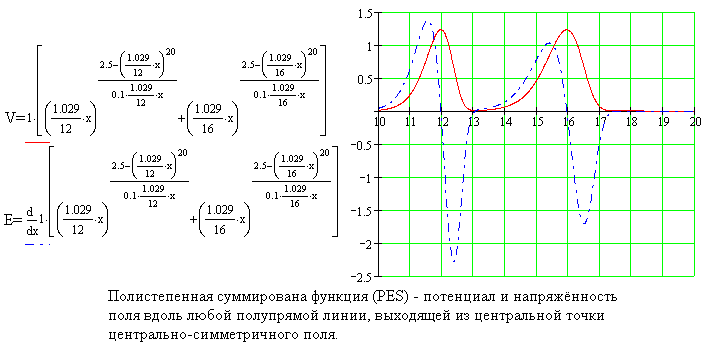
Функция PE характерна тем, что при её помощи можно описывать центрально-симметричное поле, которое имеет только одну потенциальную оболочку. При большем расстоянии от центральной точки частицы (ц.с. поля) функция изменяется подобным образом, как гравитационная функция, то есть, изменяется приблизительно обратно пропорционально квадрату расстояния. Функция PES служит для описания ц.с. полей, имеющих много потенциальных оболочек