Также факты, которые касаются фундаментальных воздействий, не требуют новых теорий, чтобы их описывать и интерпретировать. Достаточно, чтобы последовательно придерживаться закона свободного падения тел, который открыл Галилей. Надо логично доходить к причинам, которых следствием являются как гравитация, существующая в таком виде, в каком её открыл Галилей, так и ежедневно наблюдаемые свойства вещества.

Перечисленых здесь фактов, касающихся физики неба и фундаментальных воздействий, физики и астрономы не знают главным образом по той причине, что они их не осознают. Попросту, они не задумываются над этими фактами, потому что у них в умах есть идеализированы версии фиктивной действительности, и они их придерживаются. Когда они начнут размышлять над этими фактами, то будет много таких, которые без трудностей откроют эти факты для себя - в том смысле, что увидят их значение.

Факт 1: Гравитационное воздействие тел - если быть точным - не есть обратно пропорциональное квадрату расстояния и гравитационный потенциал тел не изменяется в соответствии с гиперболической функцией.

Сегодня физика учит, что гравитационное воздействие или, по-другому, гравитационное ускорение, которое является сущностью закона всемирного тяготения Ньютона, изменяется по формуле:

,

,

.

Ось ДИПО: Для описания формы орбит двух кружащих около себя тел и связанных с ними движительных явлений будет нужно новое понятие - ось ДИПО. Ось ДИПО это укороченная версия названия «ось деформации и передвижения орбит». Это определение касается особенно такой ситуации, когда два небесные тела кружат друг около друга, обладают разными массами и орбиты есть круговые*) или эллиптические. Тогда происходит передвижение орбит друг относительно друга и именно это передвижение орбит и расположение больших осей эллиптических орбит существует вдоль оси ДИПО.

Есть ситуации, когда в системе орбит ось ДИПО не существует. Эту ось невозможно определить тогда, если нет ни передвижения двух орбит друг относительно друга, ни эллиптических орбит, потому что обе орбиты есть круговые. Особенно, нет передвижения орбит в фиктивной ситуации, о которой можно теоретически рассуждать, но её не может быть в природе. А именно, передвижения орбит нет в ситуации, когда центральное тело имеет некоторую массу, а небесное тело, кружащее по орбите, имеет нолевую массу.

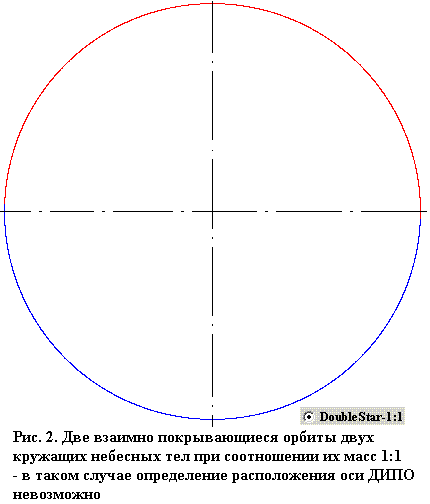
Но существует также совсем реальная ситуация, когда невозможно вычертить ось ДИПО. Эта реальная ситуация отсутствия оси ДИПО в системе круговых орбит двух кружащих друг около друга тел имеет место тогда, когда орбиты взаимно перекрываются. Такое происходит, когда массы обоих кружащих тел есть одинаковы. Две перекрывающиеся друг с другом орбиты представлены на Рис. 2.

На оси ДИПО постоянно находится результирующий центр масс обоих кружащих тел. А отдельные центры масс тел во время их орбитального движения лежат на оси ДИПО в двух временных моментах. А именно, на оси ДИПО центры тел находятся тогда, когда тела находятся наиболее близко друг друга и когда они наиболее отдалены друг от друга. Это также означает, что на оси ДИПО находятся две точки, которые принадлежат, одна одной орбите, а вторая второй, и между которыми наибольшее расстояние.

Роззеточная орбита: Для описания формы орбит двух кружащих около себя тел и связанных с ними движительных явлений будет нужно новое понятие - роззеточная орбита. Роззеточная орбита это траектория движения тела, которое воздействуя с другим телом, кружит по дороге, которой форма подобна кругу или эллипсу. Деформация дороги имеет такой характер, как бы тело двигалось по кругу или эллипсе при одновременном вращательном движении оси ДИПО. Таким образом тело после выполнения одного кружения по орбите не попадает на дорогу, по которой проходило раньше, как это происходит в случае круговых или эллиптических орбит. Вместо этого тело вычерчивает новую дорогу, которая имеет форму предыдущей дороги, а эта новая дорога есть передвижена относительно предыдущей на некоторый угол. Угол передвижения следующих фрагментов орбит, которые вычерчиваются при следующих кружениях, можно связывать с вращательной скоростью оси ДИПО.

В случае Солнечной Системы явление изменений расположения планетных орбит во вращательном движении вокруг Солнца часто называют прецессией перигелия. Это есть именно то явление, во время течения которого в более длинном временном диапазоне происходит движение небесного тела по роззеточной орбите. Хотя в более коротком временном диапазоне считается, что орбиты кружения вокруг Солнца есть эллиптические.

Из всех планет Солнечной Системы наибольшую вращательную скорость оси ДИПО имеет Меркурий. В википедии (польская версия) можно прочитать: «Пертурбации меркурианского перигелия есть незначительны -  дрейф равен 42,98 угловых секунд на столетие, то есть, для полного вращения эллипса нужно свыше 12 миллионов орбит. Подобный, хотя меньший эффект выступает в случае других небесных тел, например, для Венеры - 8,62”/столетие, для Земли - 3,84”/столетие и для планетоида 1566 Икар - 10,05”/столетие.»

Факт 2: Упущение ошибочного характера зависимости, которая описывает гравитационное воздействие, а которую то зависимость представил Исаак Ньютон, и трактование её как зависимости, которая обладает точным характером, является причиной серьёзных последствий.

Предложенная Исааком Ньютоном зависимость, которая служит для описания гравитационного воздействия и является корнем закона всемирного тяготения, трактуется в физике с некой осторожностью - до некоторой степени существует память о её приблизительном характере. Но эта осторожность касается малых расстояний от тел. А при больших расстояниях, в рассуждениях о гравитационных воздействиях принимаеся, что небесные тела являются точечными объектами. Таким способом упускаются неточности, которые вытекали бы по поводу неравномерного распределения массы в объёме небесного тела. Однако это не вяжется с трактовкой формулы Ньютона, которая касается закона всемирного тяготения, как неточной, то есть, как той формулы, которая не описывает фактически существующих гравитационных воздействий.

Несмотря на то, что эта формула «неразлучно связана с сопровождающей её ошибкой», она трактуется как точная. Это тянет за собой такие последствия, что обнародованы «неточности» в вычислениях траекторий планет не считаются результатом неточности, какая существует между математической формулой, которая описывает гравитационные ускорения, а гравитационными ускорениями, существующими в действительности. Изменения расположения большой оси эллиптической орбиты, которые, например, имеют место в случае Меркурия, а выступают в виде вращения этой оси в плоскости орбиты, не считаются - в смысле ожиданий, касающихся поведения такой эллиптической орбиты(!) – быть результатом различия мужду сегодняшними знаниями физиков и астрономов о изменениях гравитационного ускорения (в зависимости от расстояния), а действительными изменениями этого ускорения в природе.

Сейчас физики и астрономы считают, что гравитационное ускорение тел изменяется обратно пропорционально квадрату расстояния от тел. Эта зависимость, если она действительно существовала бы, вяжется с другой зависимостью, какая существует в орбитальном движении тел. А именно, в таком случае, когда два тела кружат друг вокруг друга таким способом, что их результирующий центр тяжести остаётся неподвижен и их орбиты есть эллиптические, расположения этих орбит и их форма остаются неизменны.

Когда выявилось различие в ожиданиях и действительности, касающееся формы и поведения орбиты Меркурия, то этот факт был итнерпретирован, как... Здесь можно бы подать ошибочную интерпретацию и копировать ошибочшые мнения, что было бы следующей ошибкой, потому здесь её заменят «три точки». Ибо нет нужды, чтобы в физике создавать лишние сущности.

Достаточно учитывать, что формула Ньютона только приблизительно описывает, каким способом изменяется гравитационное ускорение тел.

Для описания гравитационных воздействий и гравитационного ускорения, вместо формулы Ньютона, можно использовать формулу с немножко другой математической структурой. А именно, гравитационное ускорение и напряжённость гравитационного поля можно записать в виде:

,

Переменность гравитационного поля, которая описывается при помощи этой формулы, более близка действительно существующей в природе, чем переменность в описании Ньютона. Ибо эта формула делает возможным как описание формы эллиптических орбит которых изменения есть незамечаемы, так и описание формы орбит, которые в своих фрагментах близкие эллиптическим, но в большем временном диапазоне создают роззеточную форму (очерчение).

Потенциал гравитационного поля описывает другая функция, чем в случае ньютоновского описания - его описывает функция Е (экспоненциальная функция):

.

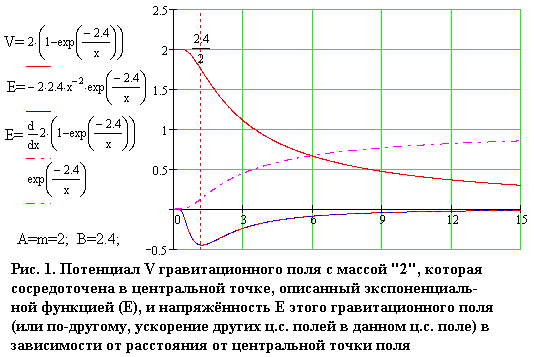
Факт 3: Тело которое движется по круговой орбите вокруг второго тела, совместно кружа с этим телом, обычно во премя этого движения не находится на одинаковом расстоянии от этого тела, а если находится, то лишь в исключительных случаях.*)

Тела, которые кружат друг около друга, будут постоянно расположены на одном расстоянии друг от друга только в том случае, когда отношение их масс будет равняться 1:1, то есть в случае, который представляет Рис. 2.*)

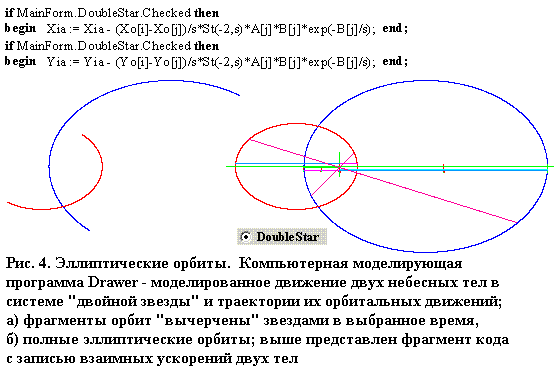
При других отношениях масс расстояние между телами во время вращения постоянно изменяется. Такое происходит, когда орбиты тел есть круговые*) и когда они есть эллиптические. Передвижения орбит и их удлинение вдоль положения оси ДИПО, в случаях, когда они круговые или эллиптические, представляют Рис. 3 и Рис. 4.

Факт 4: Если измерения указывают на существование циклических изменений расстояний между двумя кружащими небесными телами, которые осциллируют между самым большим и самым малым расстояниями (как, например, в случае Земли и Луны), то тела не всегда движутся по эллиптическим траекториям.*)

Как вытекает из зависимости между формой орбит и их передвижением, которая представлена на Рис. 3, такие изменения расстояний между орбитирующими небесными телами могут происходить также при круговой форме орбит.*) Уверенность в действительной форме орбит можно приобрести только после приравнения орбитальных скоростей тел в разных местах орбит.

Факт 5: В фокусе эллиптической орбиты вовсе не находится второе небесное тело, вокруг которого кружит первое тело, движущееся по этой орбите.

Если внимательно приглядеться законам Кеплера, то можно заметить, что - трактуя вещь точно - они не касаются какой-либо реальной, действительно существующей астрономической ситуации и её не описывают - они касаются фиктивной ситуации. Фиктивный характер ситуации возникает таким способом, что Солнце, а точнее, его центр, помещается в фокусе эллипса, который является траекторией движения планеты. А такая ситуация в действительности не существует.

Об ошибке, существующей в описании движения тел по эллипсе можно убедиться, анализируя фактическое отношение масс обоих орбитирующих небесных тел, их относительное расположение и пропорции расстояния тел от общего центра масс, существующие во время движения по эллиптическим орбитам. Используя Рис. 3 и Рис. 4, можно заметить, что никакое из тел не может быть расположено в каком-то особенном месте, которое было бы связано с орбитой второго тела. Потому что форма обоих орбит, при отдельном рассматрении каждой из них, зависит от отношения масс этих тел и от их скоростей на орбитах, а не зависит от параметров только одного тела. Конечно, форма орбит зависит тоже от взаимных ускорений, которые связаны с массами тел. А в образах и описаниях орбит, о которых рассуждается в теории, они ещё зависимы от математической формулы, которая описывает гравитационное ускорение тел.

Следовательно, как центры круговых орбит,*) так и фокусы эллиптических орбит не являются местами, которые характеризовались бы какими-то особенными приметами, кроме того, что это есть центры кругов и фокусы эллипсов.

Несмотря на то, что можно сомневаться в точной формулировке законов Кеплера, содержащиеся в них соотношения, касающиеся геометрических и физических зависимостей, есть правильны. Об этом можно убедиться,*) наблюдая круговые орбиты и поведение тел в компьютерных моделях, которых работу можно включить при помощи компьютерной моделирующей программы „Drawer” - http://www.pinopa.narod.ru/Drawer.exe .

Орбитирующие тела движутся по окружностям равномерно и ведут себя так, как бы в направление центра (каждой) окружности действовало центростремительное ускорение. Тогда как в действительности фактическое ускорение не есть центроускорительное, то есть, направленное в сторону центра круга. Ибо оно в каждый момент направлено в сторону результирующего центра массы, который отдален от центра круга.*)

Такое поведение тел не совпадает с сегодняшними знаниями на тему того, как они должны вести себя, и в некоторых случаях может стать причиной ошибки. Ибо если кто-то, учитывая форму орбит, их радиусы и орбитальные скорости тел, станет вычислять фактические ускорения тел, то получит ошибочный результат. Потому что он будет вычислять ускорения, которые в действительности не существуют. Потому что в направление центра орбиты нет никакого воздействия, которое было бы причиной ускорения тела в это направление.*)

Подобным образом обстоит дело ускорений в случае эллиптических орбит. Там тоже форма эллипса подсказывает существование воздействия на орбитирующее тело и их ускорение в направление фокуса эллипса. Тем временем действительные воздействия и ускорения направлены в сторону результирующего центра массы тел, а этот центр находится вдали от фокуса.

Факт 6: Причиной прецессионного движения орбит кружащих небесных тел является переменность гравитационного ускорения тел (напряжённости гравитационного поля тел), существующая при изменении расстояния от их центров, которая то переменность протекает немножко по-другому, чем при обратной пропорциональности квадрату расстояния.

Для разумения явления формирования двух роззеточных орбит, которое существует во время кружения двух тел, может помочь компьютерная моделирующая программа „Drawer”. В этой программе для описания и моделирования движения небесных тел использовалась функция напряжённости гравитационного поля в виде:

.

Переменность положения орбит двух кружащих тел иллюстрируют рисунки: Рис. 5а, 5б, 5в, 5г. Эти орбиты как траектории, которые тела вычерчивают во время одного вращения, своей формой подобны кругу (или эллипсу). Но точную форму круга (эллипса) они могли бы иметь только тогда, если бы напряжённость гравитационного поля была точно(!) обратно пропорциональна квадрату расстояния.

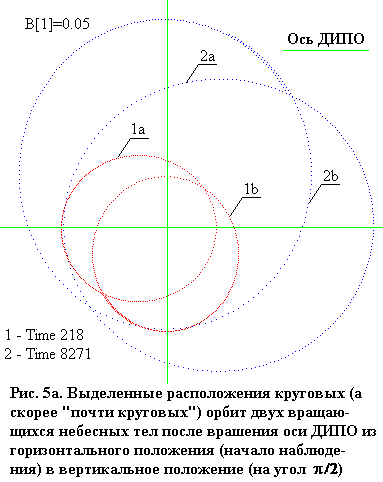
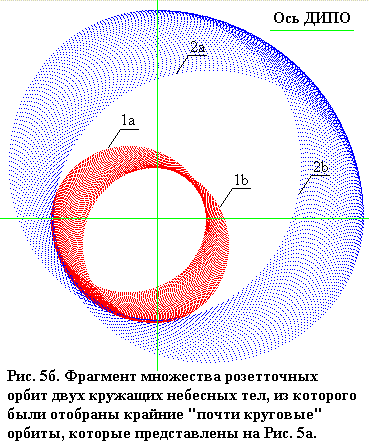
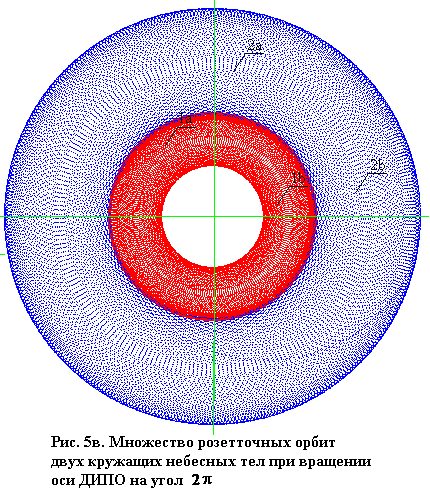
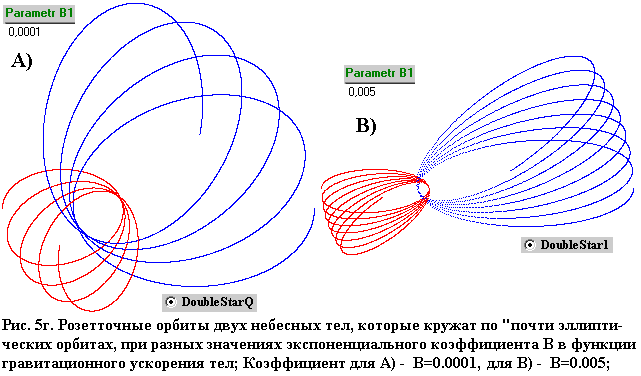
Вращение оси ДИПО системы двух «почти» круговых (а в других случаях «почти» эллиптических) орбит и в более длинном временном диапазоне формирование роззеточных орбит свидетельствует о существовании напряжённости гравитационного поля, которая отличается от версии, которую представил Ньютон.

Экспоненциальный коэффициент exp(-B/x), который существует в функции напряжённости гравитационного поля и который можно считать прибавлением к «формуле Ньютона», выясняет, почему орбиты не есть «идеально» круговые и эллиптические. Ибо он дает возможность получать в моделированых ситуациях такие орбит, которые подобны действительно существующим орбитам.

В исправленной версии закон всемирного тяготения звучит следующим образом: Между любой парой тел, которые обладают массой, существует воздействие - сила, которая действует на линии, которая проходит через их центры, а значение этой силы есть обратно пропорционально квадрату расстояния между ними и прямо пропорционально их массам и экспоненциальному коэффициенту exp(-B/x), который связан с расстоянием x между ними.

Экспоненциальный коэффициент exp(-B/x), который существует в функциях потенциала и напряжённости гравитационного поля, это хорошее обоснование и выяснение как для существования роззеточных орбит, так и для часто выступающих в природе зависимостей, которым можно приписать экспоненциальный характер.

Факт 7: Автономическое гравитационное воздействие небесных тел, которое было открыто Галилеем и представлено в законе свободного падения тел в гравитационном поле, является тождественным воздействию, которое существует при любом расстоянии от тел, от самых больших до самых малых, и этот автономический характер воздействия всех тел не зависит от их массы и величины. То есть, он существует при воздействии небесных тел и атомов, при космических и междуатомных расстояниях.

Автономический характер воздействия заключается в том, что ускорение, которое одно тело прибавляет второму, никаким образом не зависит от параметров этого второго тела. Автономический характер не изменяется, если из этого тела «всё другое выбросить», а брать во внимание только один атом и ускорение, какое он прибавляет второму телу или второму атому. Также в этом случае ускорение других объектов будет зависеть только от массы этого атома.

Получается так потому, что ведь это атомы придают характер и свойства макроскопическим телам. Ибо в состоящих из атомов макроскопических телах не может существовать какое-либо их свойство, которое не происходило бы от свойств, какими обладают атомы.

По той причине, что это есть новый способ трактовки задачи в физике, воздействие между атомами и другими объектами в макро и микромасштабе можно записать в виде нового физического закона - закона автономического воздействия атомов. Закон автономического воздействия атомов гласит: Как при малых, так и при больших расстояниях, ускорение, которое один атом прибавляет второму атому или другим объектам (например, химическим частицам), никаким образом не зависит от параметров ускоряемых объектов.

Стоит сформулировать этот закон и иметь его во внимании, потому что он особенно подчеркивает, что автономическое воздействие (его характер) не зависит от величины тел и расстояния между ними. Оно начинается на том уровне строения вещества, где имеем дело с атомами, нейтронами, электронами и гипотетическими фундаментальными частицами, а кончится на уровне, где выступают туманности, галактики итд.

Автономическое ускорение тел - а конкретно, характер его изменения - независимо от того, будет ли то планета или атом, непосредственно связано с напряжённостью поля. Как в случае планеты, так и атома, связанное с ними поле располагается во всей вселенной. То есть, оно существует очень далеко от этих объектов и существует очень близко них. При больших расстояниях функция, по которой протекает воздействие, есть известна и определена в законе гравитационного тяготения. При меньших расстояниях функция, по которой протекает воздействие, есть другая и требует исследования. Однако, чтобы можно было начать такие исследования, должна измениться научная парадигма, которая связана с физикой неба и фундаментальными воздействиями и которая господствует в мышлении учёных.

Сейчас только ориентировочно можно определить, каким характером обладают математические функции, которые описывают автономические ускорения атомов при малых расстояниях. Этот характер уже определен и включен в код компьютерной моделирующей программы „Drawer”. При помощи этой программы можно увидеть (в моделированной ситуации), например, траектории движения двух атомов, которые колебаются друг относительно друга и одновременно выполняют вращательное движение. Эти траектории до некоторой степени подобны роззеточным орбитам, следовательно, об этих атомах тоже можно сказать, что кружат по роззеточным орбитам.

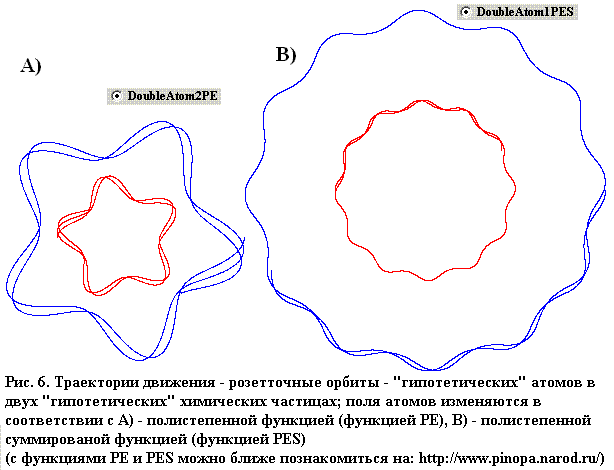
Факт 8: При учитывании автономического воздействия таких элементов вещества, как атомы, нейтроны, электроны, а также гипотетические фундаментальные элементы, и пользуясь подходящими математическими функциями, которые описывают напряжённости полей этих элементов, можно создать модели стабильных вещественных структур и протекающих в веществе явлений.

В таких случаях проблему точности отображения происходящих в природе явлений решает выбор подходящих функций напряжённости поля, достаточно сложная моделирующая программа, которая позволяет записывать в ней все участвующие в явлениях частицы, и достаточно сильный компьютер.

Сейчас уже есть отработаны простые модели колебающихся струн и стержней, есть модели явлений, связанных с вращающимся гироскопом, модели контактного потенциала и течения электрического тока, модели электромагнитных явлений, есть модели планетных систем и связанных с ними явлений, есть модели кристаллических структур.

Отработка модели заключается в выборе подходящих частиц, приписании им подходящих параметров, которые касаются их поля, распределения в пространстве и начальных скоростей. Умение замечать физическое явление в движении нескольких, нескольких десятков или нескольких сотней частиц зависит от знаний и интерпретационных умений особы, которая наблюдает движение частиц. Но при некоторой практике можно не только делать некоторого рода наблюдательный синтез и видеть известные физические явления, но также замечать и открывать неизвестные, новые физические явления.

Вместо эпилога.
Характер этой статьи такого рода, что Автор, хочет он этого или нет, выступает в роли того, кто «исправляет» Кеплера, Ньютона и Ейнштейна. Читатели могут иметь к Автору претенсии о многие вещи. Они могут думать, что Автор важничает, что философствует, что не уважает Авторитетов, что крушит упорядоченный мир научных мнений Читателей. Имея это ввиду, Автор заранее просит извинения за всякие психические невыгоды, какие возникли вследствие чтения этой статьи, и советует, чтобы не думали, о чём здесь прочитали, и в короткое время об этом забыли, а тогда вернётся спокойствие.

Остальных Читателей Автор просит, чтобы повторно прочитали эту статью и над каждым из перечисленных здесь фактов глубоко задумались. А при случае, когда у них будет свободное время, могут на страницы http://pinopa.narod.ru/ познакомиться с другими статьями из области фундаментальной физики.

*     *     *

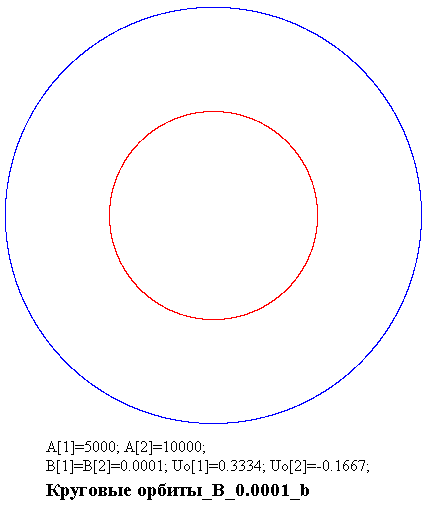
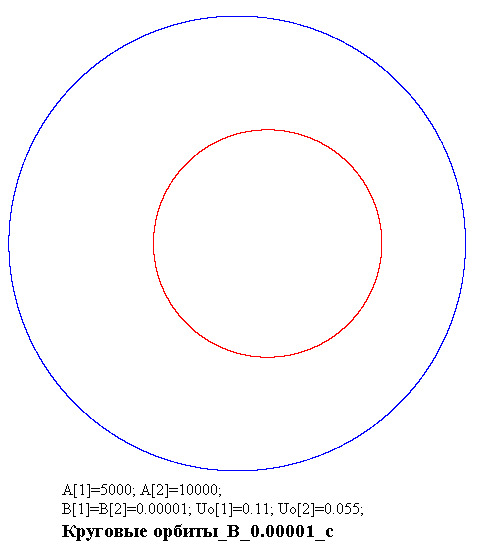
На рисунках, в названиях которых (в конце) находится буква "а" и "с" видно смещение орбит - на рисунке с буквой "а": внутренняя орбита перемещена "влево" относительно внешней орбиты, а на рисунке с буквой "с": внутренняя орбита перемещена "вправо" относительно внешней орбиты. Сравнение скорости двух орбитирующих тел в ситуациях, которые представлены на рисунках "а" и "с", в обоих группах рисунков, подказывает, что существует "промежуточная" скорость тел на орбите, при которой их орбиты располагаются концентрично относительно друг друга, то есть, орбиты не смещены относительно друг друга ни в одну, ни в другую сторону.
Приблизительным способом (с незаметным смещением и очень небольшой погрешностью) эти (почти идеальные) ситуации представлены на рисунках, которые в конце названия имеют букву "b".
Для первой группы и для тела [1] мы имеем данные: для "а" мы имеем Uo [1] = 0,3 и для "с" имеем Uo [1] = 0,34, а для тела [2] имеем скорости (их абсолютные значения) в два раза меньше, а именно: для "а" у нас есть Uo [2] =- 0,15 и для "с" есть Uo [2] =- 0,17. Для "b" имеем Uo [1] = 0,3334 и Uo [2] =- 0,1667, то есть, мы имеем некоторые промежуточные значения.
Подобным образом дело выглядит для второй группы рисунков, где для тела [1] имеем данные: для "а" имеем Uo [1] = 0,1 и для "с" имеем Uo [1] = 0,11, а для тела [2] мы имеем скорости (их абсолютные значения) в два раза меньше, а именно: для "а" у нас есть Uo [2] =- 0,05 и для "с" Uo [2] =- 0,055. Для "b" мы имеем Uo [1] = 0,1054 и Uo [2] =- 0,0527.
(Символы "+" и "-" при значениях скорости символизируют расположение вектора скорости в некоторый момент времени в системе координат относительно оси Z.)
 
 

На рисунке KO_B_0.0000001 есть представлены круговые орбиты двух тел, кружащих друг вокруг друга. Эти орбиты имеют идентичные радиусы, как орбиты кружащих двух тел, которые представлены на рисунках KO_B_0.0001_b  и  KO_B_0.00001_b. Потому что ситуации с орбитирующими друг вокруг друга двумя телами (в каждом из этих трех случаев) были смоделированы с тем же начальным (в начале моделируемого процесса) расположением тел друг относительно друга. Разные были только значения экспоненциального коэффициента В и начальные скорости. Но каждый раз эти скорости выбирались таким образом, чтобы круговые орбиты получились по возможности наиболее близкие идеалу. Здесь можно заметить, что отношения в моделируемых ситуациях есть подобны независимо от того, подлежит ли изменению экспоненциальный коэффициент В или коэффициент пропорциональности А. Например, если А или B увеличить стократно, тогда чтобы получить идентичную форму орбит, надо орбитальную скорость тел увеличить в десять раз. Если коэффициент А увеличить в сто раз и коэффициент B уменьшить в сто раз (или наоборот), то орбиты тел останутся без изменения, следовательно, нет необходимости менять скорости объектов на орбите.

Представленный выше рисунок в некоторой степени выясняет, что аналитическое исследование отношений между расстояниями кружащих тел от общего центра массы, когда они кружат по круговым орбитам, не защищает перед ошибочным сочетанием. Теоретически, два тела могут кружить друг относительно друга по круговым орбитам, которые смещены друг относительно друга. Но это должна позволять ускорительная математическая функция, по которой происходит взаимное ускорение тел. (Потому что от характера этих воздействий зависит, будут ли орбиты круговыми, эллиптическими или ещё другими.) Однако тела воздействуют друг с другом по такой математической функции, которая на это не позволяет.